Олимпиадная задача по алгебраическим неравенствам: последовательности, индукция, 1–2 класс
Задача
Последовательности положительных чисел (xn) и (yn) удовлетворяют условиям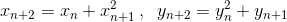 
при всех натуральных n. Докажите, что если все числа x1, x2, y1, y2 больше 1, то xn > yn при каком-нибудь натуральном n.
Решение
Очевидно, начиная со второго члена, наши последовательности возрастают: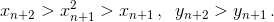 
Так как x3 > 1 + 1² = 2,
y3 > 1² + 1 = 2, все члены каждой из последовательностей, начиная с третьего, больше 2. Аналогично при n > 3 получим xn > 3, yn > 3.
Заметим теперь, что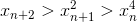 
при n > 1. С другой стороны, 
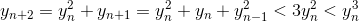при n > 3. Итак, при n > 3 имеем 
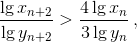а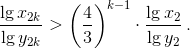 
При достаточно большом k правая часть последнего неравенства больше 1, а значит, x2k > y2k.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет