Олимпиадная задача по многочленам и неравенствам: докажите неравенство для b

  Обозначим через c₁ и c₂ корни уравнения  f(x) = 0,  а через x₁ и x₂  – корни уравнения  f(f(x)) = 0,  сумма которых равна  –1. Множество корней последнего уравнения совпадает с объединением множеств корней уравнений  f(x) = c₁  и  f(x) = c₂.  Рассмотрим два случая.

  1)  x₁ и x₂ являются корнями одного из последних двух уравнений. Тогда их сумма равна – a, откуда  a = 1.  Можно считать, что  c₁ ≥ c₂.  Поскольку

c₁ + c₂ = –1,  то  c₂ ≤ – ½.  Из условия следует, что дискриминант уравнения  f(x) = c₂  положителен, то есть  1 – 4b + 4c₂ > 0.  Отсюда  4b < 1 + 4c₂ ≤ –1.

  2)  x₁ – корень уравнения  f(x) = c₁,  а x₂ – корень уравнения  f(x) = c₂.  Тогда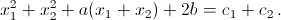  

  Поскольку  c₁ + c₂ = – a,  а  x₁ + x₂ = –1,  то 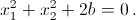    Но тогда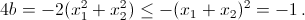   

Ответ задачи отсутствует