Олимпиадная задача по стереометрии: прямоугольный параллелепипед и шестиугольник
Задача
В прямоугольном параллелепипеде одно из сечений является правильным шестиугольником. Докажите, что этот параллелепипед – куб.
Решение
Достроим шестиугольник до правильного треугольника (см. рис.).
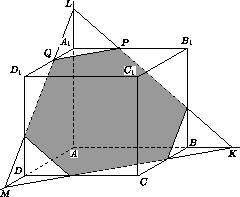
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет