Олимпиадная задача по математике: натуральные n для многочленов, 10–11 класс
Задача
Найдите все такие натуральные n, что при некоторых различных натуральных a, b, c и d среди чисел
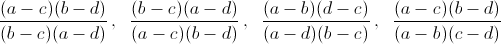
Решение
Пусть 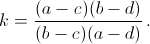 Тогда
Тогда 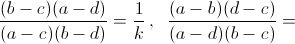
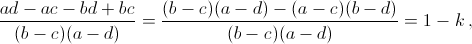
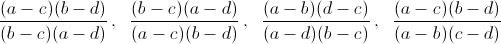 Пусть два из этих чисел равны натуральному числу n. В парах (k, 1 – k), (1/k, 1 – k), (1/k, k/k–1), (1 – k, k/k–1) оба числа не могут быть натуральными одновременно. Остаются два случая:
k = n и либо n = 1/n, либо n = n/n–1.
Пусть два из этих чисел равны натуральному числу n. В парах (k, 1 – k), (1/k, 1 – k), (1/k, k/k–1), (1 – k, k/k–1) оба числа не могут быть натуральными одновременно. Остаются два случая:
k = n и либо n = 1/n, либо n = n/n–1.
В первом случае k = n = 1, значит, 1 – k = 0 ⇔ (a – b)(d – c) = 0, и тогда среди чисел a, b, c и d были бы равные.
Во втором случае n = 2. Это значение принимается, например, при a = 1, b = 3, c = 4, d = 7.
Ответ
n = 2.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет