Олимпиадная задача по стереометрии и комбинаторной геометрии для 10–11 классов от Рубанова И.С.

Впишем в цилиндр правильный треугольник с вершинами в серединах образующих и рассмотрим три единичных шара с центрами в серединах его сторон. Возьмем основание цилиндра. С ним наши шары пересекаются по трем кругам радиуса 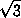/2с центрами в серединах сторон вписанного правильного треугольника. Легко проверить, что эти три круга целиком покрывают основание. Значит, цилиндр целиком покрыт тремя цилиндрами высоты 1, построенными на этих кругах, а, следовательно, и нашими шарами, содержащими эти цилиндры.

Чтобы показать, что двумя шарами покрыть цилиндр не удастся, достаточно заметить, что если центр шара не совпадает с центром основания, то круг, по которому шар пересекается с плоскостью основания, пересекается с границей основания по дуге, меньшей180^o , а двумя такими дугами окружность не покрыть. Если же центры двух шаров совпадают с центрами оснований, то непокрытой остается боковая поверхность цилиндра.

Тремя.