Олимпиадная задача Храброва: неограниченность числовой последовательности — 9–11 класс
Задача
По данному натуральному числу a0 строится последовательность {an} следующим образом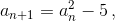 
если an нечётно, и a0/2, если an чётно. Докажите, что при любом нечётном a0 > 5 в последовательности {an} встретятся сколь угодно большие числа.
Решение
Пусть число an = 2k + 1 нечётно и больше 5. Тогда an+1 = (2k + 1)² – 5 = 4k² + 4k – 4, an+2 = 2k² + 2k – 2 и an+3 = k² + k – 1. При этом an+3 нечётно и, поскольку k > 2, то an+3 = k² + k – 1 > 2k + 1 = an. Таким образом, a0 < a3 < a6 < ... < a3m, поэтому при любом n имеем a3n ≥ n.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет