Олимпиадная задача по планиметрии и комбинаторной геометрии для 7–10 классов
Задача
На плоскости расположено[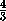 n]прямоугольников со
сторонами, параллельными осям координат. Известно, что любой прямоугольник
пересекается хотя бы с n прямоугольниками. Доказать, что найдется
прямоугольник, пересекающийся со всеми прямоугольниками.
n]прямоугольников со
сторонами, параллельными осям координат. Известно, что любой прямоугольник
пересекается хотя бы с n прямоугольниками. Доказать, что найдется
прямоугольник, пересекающийся со всеми прямоугольниками.
Решение
Обозначим число прямоугольников через k . Рассмотрим самую нижнюю из верхних границ прямоугольников (назовем прямую, на которой она лежит, d , а сам прямоугольник – P ). Есть не более, чем k-n-1прямоугольников таких, что их нижняя граница лежит выше d , так как все такие прямоугольники не пересекаются с P . Назовем эти прямоугольники нижнеплохими. Аналогично определим верхнеплохие, левоплохие и правоплохие прямоугольники.
Заметим, что поскольку k>4 x (k-n-1)(это равносильно3k<4n+4), то существует прямоугольник A , не являющийся нижне-, верхне-, лево- или правоплохим. Но тогда он пересекается со всеми прямоугольниками.
В самом деле: пусть с ним не пересекается какой-то прямоугольник B , тогда либо какая-то горизонтальная, либо какая-то вертикальная прямая разделяет B и A . Если, например, онa горизонтальна и прямоугольник A лежит выше нее, то верхняя граница B лежит ниже нижней границы A , что невозможно по построению. Остальные три случая аналогичны.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь