Олимпиадная задача по стереометрии: высота параллелепипеда, середина ребра и перпендикулярные прямые
Задача
Точка M – середина бокового ребра AA1параллелепипеда ABCDA1B1C1D1. Прямые BD , MD1и A1C попарно
перпендикулярны. Найдите высоту параллелепипеда, если BD=2a , BC=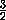 a , A1C=4a .
a , A1C=4a .
Решение
Рассмотрим сечение данного параллелепипеда плоскостью, проходящей
через точки B1, D1и M (рис.1). Прямая A1C перпендикулярна
этой плоскости, поскольку A1C 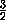 MD1и A1C
MD1и A1C 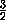 B1D1(т.к. A1C
B1D1(т.к. A1C 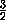 BD , а B1D1 || BD ).
BD , а B1D1 || BD ).
Пусть K – центр параллелограмма A1B1C1D1. Плоскости B1MD1и ACC1A1пересекаются по прямой MK , значит, прямая A1C пересекает
сечение B1MD1в некоторой точке Q , лежащей на отрезке MK , причём 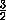 A1QD1 = 90o , т.к. прямая D1Q лежит в плоскости B1MD1,
перпендикулярной A1C .
A1QD1 = 90o , т.к. прямая D1Q лежит в плоскости B1MD1,
перпендикулярной A1C .
Пусть O – точка пересечения диагоналей паралелограмма ACC1A1. Заметим, что MK – средняя линия треугольника AA1C , а т.к. A1O – медиана этого треугольника, то Q – общая середина отрезков A1C и MK . Значит,
A1Q=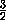 A1O =
A1O = 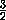 A1C =
A1C = 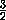 · 4a = a.
· 4a = a.
D1Q = 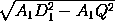 =
= 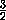 =
=
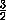 =
= 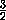 .
.
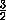 MD1B1 = 90o , т.к. D1M
MD1B1 = 90o , т.к. D1M 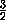 BD , а B1D1 || BD . Значит, D1Q – медиана прямоугольного треугольника MD1K (рис.2), проведённая из вершины прямого угла. Поэтому MK=2D1Q = a
BD , а B1D1 || BD . Значит, D1Q – медиана прямоугольного треугольника MD1K (рис.2), проведённая из вершины прямого угла. Поэтому MK=2D1Q = a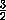 ,
а т.к. D1K =
,
а т.к. D1K = 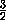 B1D1 =
B1D1 = 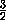 BD =
BD = 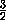 · 2a = a , то
· 2a = a , то
D1M = 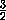 =
= 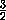 = 2a.
= 2a.
V1 = 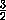 ·
· 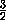 B1D1· D1M · A1Q =
B1D1· D1M · A1Q =
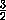 ·
· 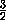 · 2a· 2a · a =
· 2a· 2a · a = 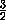 a3.
a3.
V=12V1 = 12· 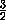 a3 = 8a3.
a3 = 8a3.
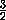 a =3a . Пусть A1H – высота этого
равнобедренного треугольника. Тогда
a =3a . Пусть A1H – высота этого
равнобедренного треугольника. Тогда
A1H = 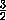 =
=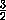 = 2a
= 2a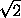 .
.
SA1B1C1D1 = SΔ A1C1P = 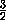 C1P· A1H =
C1P· A1H =
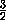 · 2a· 2a
· 2a· 2a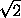 = 2a2
= 2a2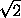 .
.
h = 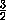 =
= 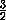 =
2a
=
2a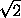 .
.
Ответ
2a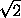 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь