Олимпиадная задача по планиметрии для 8–9 класса: точки K и M в треугольнике
Задача
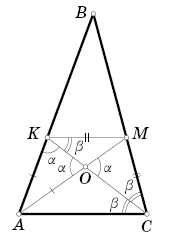
На сторонах AB и BC треугольника ABC выбраны точки K и M соответственно так, что KM || AC. Отрезки AM и KC пересекаются в точке O. Известно, что AK = AO и KM = MC. Докажите, что AM = KB.
Решение
Пусть ∠AKO = ∠AOK = ∠MOC = α, ∠MKC = ∠MCK = ∠ACO = β (рис. слева). Далее можно рассуждать по-разному. Первый способ. В треугольниках KCA и OCM две пары соответственно равных углов, поэтому и третьи углы равны: ∠CAK = ∠CMO = ∠AMC. Заметим, что ∠MKB = ∠CAK и ∠ACM = ∠KMB. Значит, треугольники AMC и BKM равны по стороне и двум углам. Следовательно, AM = KB.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет