Олимпиадная задача по планиметрии: точки A, B, C, D на одной окружности
Задача
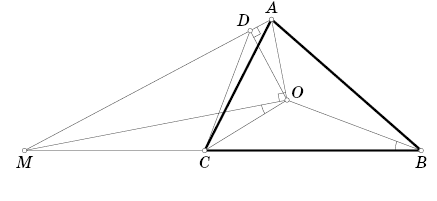
Через центр O вписанной в треугольник ABC окружности проведена прямая, перпендикулярная прямой AO и пересекающая прямую BC в точке M.
Из точки O на прямую AM опущен перпендикуляр OD. Докажите, что точки A, B, C и D лежат на одной окружности.
Решение
Так как OD – высота прямоугольного треугольника MAO, то MO² = MA·MD (см. рис.).
∠AOC = 90° + ∠OBC > 90°. Отсюда ∠MOC = ∠AOC – 90° = ∠OBC, и треугольники MOB и MCO подобны (угол OMC – общий). Следовательно,
MO : MC = MB : MO, откуда MO² = MB·MC. Из равенства MA·MD = MB·MC следует, что точки A, B, C и D лежат на одной окружности.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет