Олимпиадная задача по планиметрии: диаметр многоугольников после разреза квадрата
Задача
Квадрат со стороной 1 см разрезан на три выпуклых многоугольника. Может ли случиться, что диаметр каждого из них не превосходит
а) 1 см; б) 1,01 см; в) 1,001 см?
Решение
а) В один многоугольник попадут две вершины квадрата, скажем A и B. Остальные точки отрезка AD удалены от B на расстояние больше 1, поэтому они находятся вне этого многоугольника, следовательно, A лежит на границе двух многоугольников (первого и второго). Аналогично B лежит на границе первого и третьего многоугольников (B не может принадлежать второму). Но тогда середина K стороны CD не может принадлежать ни одному из многоугольников. Противоречие. б) Разобьём квадрат на прямоугольник 1×⅛ и два прямоугольника ½×⅞ . Их диагонали (диаметры) равны и меньше 1,01:
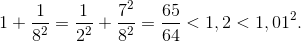 в) Предположим нам удалось разрезать квадрат на три многоугольника M1, M2, M3 нужных диаметров. Пусть вершины A и B принадлежат M1. Отложим на стороне AD отрезок AG = 0,05, а на стороне BC – отрезок BH = 0,1. Точки G и H не могут принадлежать M1, поскольку AH > BG > 1,001. Пусть G принадлежит M2. Тогда H принадлежит M3 (HG = BG > 1,001), а середина K стороны CD не может принадлежать ни одному из многоугольников: AK > GK > HK > 1,001. Противоречие.
в) Предположим нам удалось разрезать квадрат на три многоугольника M1, M2, M3 нужных диаметров. Пусть вершины A и B принадлежат M1. Отложим на стороне AD отрезок AG = 0,05, а на стороне BC – отрезок BH = 0,1. Точки G и H не могут принадлежать M1, поскольку AH > BG > 1,001. Пусть G принадлежит M2. Тогда H принадлежит M3 (HG = BG > 1,001), а середина K стороны CD не может принадлежать ни одному из многоугольников: AK > GK > HK > 1,001. Противоречие.
Ответ
а), в) Не может; б) может.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь