Олимпиадная задача по планиметрии для 8-9 класса: равенство отрезков и угол в треугольнике
Задача
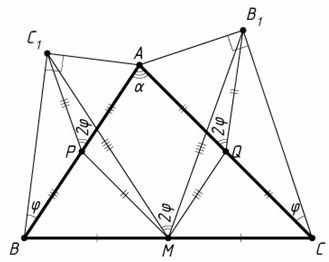
На сторонах AB и AC треугольника ABC внешним образом построены прямоугольные треугольники ABC1 и AB1C, причём ∠C1 = ∠B1 = 90°,
∠ABC1 = ∠ACB1 = φ; M – середина BC. Докажите, что MB1 = MC1 и ∠B1MC1 = 2φ.
Решение
Пусть P и Q – середины сторон AB и AC соответственно. Тогда APMQ – параллелограмм. B1Q и C1P – медианы прямоугольных треугольников AB1C и ABC1, поэтому ∠B1Q = ∠AC = AQ = PM, MQ = AP = ½ AB = C1P, ∠MQB1 = ∠MQA + ∠AQB1 = ∠MQA + 2φ,
∠C1PM = ∠APM + ∠APC1 = ∠APM + 2φ = ∠MQA + 2φ = ∠MQB1.
Значит, треугольники MQB1 и C1PM равны по двум сторонам и углу между ними. Следовательно, MB1 = MC1. Обозначим ∠A = α. Тогда
∠B1MC1 = ∠PMQ – (∠QMB1 + PMC1) = α – (∠QMB1 + ∠MB1Q) = α – (180° – ∠MQB1) = α – 180° + ∠MQB1 = α – 180° + (180° – α + 2φ) = 2φ.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь