Назад

Олимпиадная задача по планиметрии для 9–11 классов: окружности и вписанные точки

Задача 211799 • Сложность: 3 • 9-11 класс
Задача

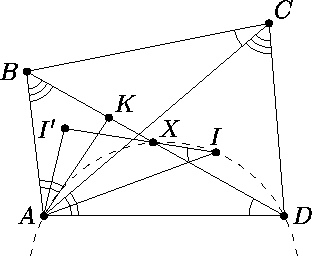
На диагонали BD вписанного четырёхугольника ABCD выбрана такая точка K, что  ∠AKB = ∠ADC.  Пусть I и I' – центры вписанных окружностей треугольников ACD и ABK соответственно. Отрезки II' и BD пересекаются в точке X. Докажите, что точки A, X, I, D лежат на одной окружности.

Решение
В треугольникахABKиACDуглыAKBиADCравны по условию, а  ∠ABK= ∠ABD= ∠ACD  как вписанные; значит, эти треугольники подобны. Следовательно, треугольникABKпереходит в треугольникACDпри поворотной гомотетии с центромA(то есть при повороте на уголBACи последующей гомотетии с коэффициентомAC/AB). При этой поворотной гомотетии точкаI'переходит в точкуI(так какI'иI– соответственные точки подобных треугольниковABKиACD), поэтому  ∠I'AI= ∠BAC  и  AI/AI' = AC/AB.  Значит, треугольникAII'подобен треугольникуACB, откуда ∠AIX= ∠AII'= ∠ACB.  Но  ∠ACB= ∠ADB,  откуда  ∠AIX= ∠ADX;  это и означает, что точкиA, X, I, Dлежат на одной окружности.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет