Олимпиадная задача по планиметрии: угол FMP в треугольнике и вписанной окружности
Задача
Вписанная в треугольник ABC окружность ω касается сторонAB и AC в точках D и E соответственно. Пусть P – произвольная точка на большей дуге DE окружности ω, F – точка, симметричная точке A относительно прямой DP, M – середина отрезка DE. Докажите, что угол FMP – прямой.
Решение
Пусть G – точка, симметричная точке A относительно прямой EP. Из симметрии PF = PA = PG, а также FD = AD, GE = AE. Поскольку AD и AE – равные отрезки касательных, FD = GE. Далее, ∠(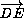 ,
, 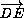 ) (угол от вектора
) (угол от вектора 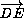 до вектора
до вектора 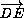 , отсчитываемый против часовой стрелки) равен
, отсчитываемый против часовой стрелки) равен
∠ADE = 2∠BDP = ∠DPE + 2∠DEP и аналогично ∠( ,
, 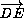 ) = ∠AED + 2∠CEP = ∠DPE + 2∠EDP. Значит,
) = ∠AED + 2∠CEP = ∠DPE + 2∠EDP. Значит,
∠(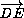 ,
, 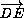 ) = ∠(
) = ∠(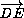 ,
, 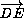 ) + ∠(
) + ∠(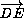 ,
, 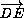 ) = (∠DPE + 2∠EDP) + (∠DPE + 2∠DEP) = 2(∠DPE + ∠DEP + ∠EDP) = 360°, то есть векторы
) = (∠DPE + 2∠EDP) + (∠DPE + 2∠DEP) = 2(∠DPE + ∠DEP + ∠EDP) = 360°, то есть векторы 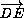 и
и 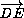 сонаправлены и равны. Следовательно, FDGE – параллелограмм. Точка M – середина диагонали DE, значит, она также является серединой диагонали FG. Следовательно, PM – медиана (а значит, и высота) равнобедренного треугольника FPG.
сонаправлены и равны. Следовательно, FDGE – параллелограмм. Точка M – середина диагонали DE, значит, она также является серединой диагонали FG. Следовательно, PM – медиана (а значит, и высота) равнобедренного треугольника FPG.
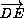
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь