Олимпиадная задача по планиметрии для 9–11 классов от Полянского А. — угол в треугольнике и вписанная окружность
Задача
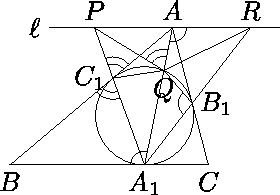
Вписанная окружность треугольника ABC касается сторон BC, AC, AB в точках A1, B1, C1 соответственно. Отрезок AA1 вторично пересекает вписанную окружность в точке Q. Прямая l параллельна BC и проходит через A. Прямые A1C1 и A1B1 пересекают l в точках P и R соответственно. Докажите, что ∠PQR = ∠B1QC1.
Решение
∠A1B1Q = ∠BA1A = ∠A1AR = ∠QAR. Значит, четырёхугольник ARB1Q – вписанный. Аналогично вписанным является и четырёхугольник PAQC1. Следовательно, ∠PQR = ∠PQA + ∠RQA = ∠PC1A + ∠RB1A = ∠A1C1B + ∠A1B1C = ∠A1QC1 + ∠A1QB1 = ∠B1QC1.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет