Олимпиадная задача по стереометрии для 10–11 класса: выбор скрещивающихся рёбер треугольной пирамиды

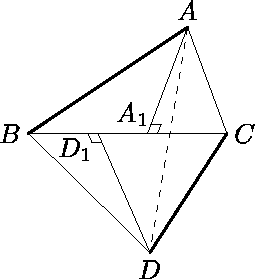
Пусть дана пирамида ABCD . Выберем пару ее скрещивающихся ребер с наибольшей суммой квадратов– пусть это AB и CD . Покажем, что шары с диаметрами AB и CD покрывают каждое ребро пирамиды. Ясно, что достаточно доказать это для ребра BC . Рассмотрим основания A₁ и D₁ перпендикуляров, опущенных соответственно из A и D на BC . Тогда AB²+CD²=AA₁²+BA₁²+DD₁²+CD₁² AC²+BD²=AA₁²+CA₁²+DD₁²+BD₁² , откуда BA₁²+CD₁² CA₁²+BD₁² . Это означает, что отрезки BA₁ и CD₁ перекрываются, а значит, они покрывают весь отрезок BC . Но наши шары как раз покрывают оба этих отрезка. Поскольку шары покрывают все ребра, то они покрывают и все грани. Пусть теперь какая-то точка X тетраэдра не покрыта шарами. Тогда из нее можно выпустить луч, не имеющий общих точек с шарами. Однако он пересечет поверхность в точке, принадлежащей одному из шаров– противоречие.

Всегда.