Олимпиадная задача по планиметрии: окружности и касательные, 9

Задача

Две окружности σ₁ и σ₂ пересекаются в точках A и B . Пусть PQ и RS – отрезки общих внешних касательных к этим окружностям (точки P и R лежат на σ₁ , точки Q и S – на σ₂ ). Оказалось, что RB|| PQ . Луч RB вторично пересекает σ₂ в точке W . Найдите отношение RB/BW .

Решение

1/3.

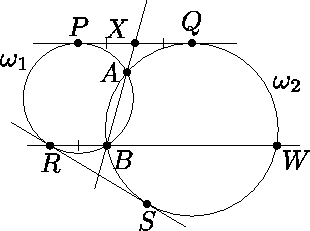
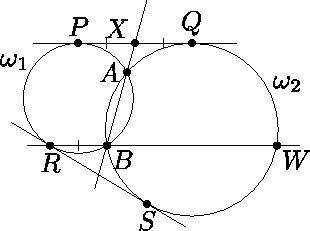Пусть X – точка пересечения прямых AB и PQ . Тогда XP²=XA· XB=XQ² , т.е. X – середина PQ . Прямые AB и PR параллельны, так как обе эти прямые перпендикулярны линии центров окружностей σ₁ и σ₂ . Из условия теперь получаем, что четырехугольник PXBR – параллелограмм, откуда BR = XP= PQ = 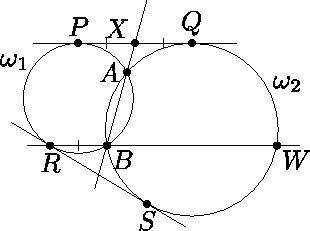RS (последнее– из симметрии PQ и RS ). Далее, так как RS – отрезок касательной к σ₂ , то RB· RW = RS²=(2RB)² , откуда RW=4RB . Значит, RB/BW = 1/3.

Ответ

Ответ задачи отсутствует

Олимпиадная задача по планиметрии: касательные к пересекающимся окружностям, 9–10 класс

Задача

Решение

Ответ

Подтверждение удаления