Олимпиадная задача по планиметрии для 8-9 классов от Берлова С. Л.
Задача
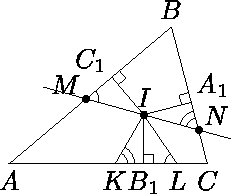
Через точку I пересечения биссектрис треугольника ABC проведена прямая, пересекающая стороны AB и BC в точках M и N соответственно. Треугольник BMN оказался остроугольным. На стороне AC выбраны точки K и L так, что ∠ILA = ∠IMB, ∠IKC = ∠INB. Докажите, что
AM + KL + CN = AC.
Решение
Опустим из точки I на стороны AB, BC, CA перпендикуляры IC1, IA1, IB1 соответственно (см. рис.). Очевидно, эти перпендикуляры равны по длине; кроме того, AC1 = AB1 и CA1 = CB1. Значит, прямоугольные треугольники IKB1 и INA1 равны по катету и острому углу, поэтому B1K = A1N. Аналогично B1L = C1M. Следовательно, AM + KL + CN = AM + MC1 + NA1 + CN = AC1 + CA1 = AB1 + CB1 = AC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет