Олимпиадная задача: оптимальное разрезание квадрата Андреем и минимизация суммы произведений
Задача
В квадрате 10×10 расставлены числа от 1 до 100: в первой строчке – от 1 до 10 слева направо, во второй – от 11 до 20 слева направо и т.д. Андрей собирается разрезать квадрат на доминошки 1×2, посчитать произведение чисел в каждой доминошке и сложить полученные 50 чисел. Он стремится получить как можно меньшую сумму. Как ему следует разрезать квадрат?
Решение
Пронумеруем доминошки разбиения. Пусть в i-й доминошке лежат числа ai и bi. Заметим, что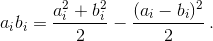 
Просуммировав эти равенства по всем доминошкам, получаем, что сумма всех 50 произведений равна 
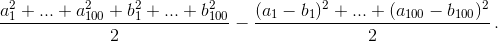Первая дробь равна ½ (1² + ... + 100²), то есть не зависит от разбиения. В числителе же второй дроби каждый квадрат равен либо 1², либо 10² – в зависимости от того, горизонтальна или вертикальна i-я доминошка. Поэтому вторая дробь будет максимальна (а итоговая сумма – минимальна) тогда, когда все слагаемые в числителе будут равняться 100, то есть когда все доминошки вертикальны.
Ответ
На 50 вертикальных прямоугольников (см. рис.).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь