Олимпиадная задача: максимум сотрудников в НИИЧАВО при посещении буфета, комбинаторика

  Пусть в НИИ в тот день работали n человек. По условию, для каждой пары сотрудников время, когда в буфете присутствовал ровно один из них, не меньше x. Суммируя все эти промежутки времени по всем парам, получим число  S ≥ ½ n(n + 1)x.

  Посчитаем это число другим способом. Отметим моменты, когда в буфет кто-то входил или из него кто-то выходил. Рабочий день разбился на m промежутков с длинами  t₁, ..., t_m.  Пусть на промежутке с номером i в буфете находилось k_i человек. Тогда этот промежуток будет посчитан ровно для тех пар сотрудников, в которых ровно один присутствует в буфете; таких пар  k_i(n – k_i).  Поэтому этот промежуток внесёт в S вклад  t_ik_i(n – k_i).  Выражение  k(n – k)  достигает максимума при  k = [ⁿ/₂],  поэтому указанный вклад не больше  t_i [ⁿ/₂](n – [ⁿ/₂]).  Поскольку  t₁ + ... + t_m = 8,  то, суммируя, получаем, что  8 [ⁿ/₂](n – [ⁿ/₂]) ≥ S ≥ ½ n(n + 1)x.

  Рассмотрим два случая.

  1)  n = 2l.  Тогда   8l² ≥ l(2l – 1)x,   то есть  (2x – 8)l ≤ x,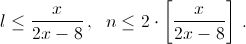  

  2)  n = 2l + 1. Тогда  8l(l + 1) ≥ l(2l + 1)x,  то есть  (2x – 8)l ≤ 8 – x,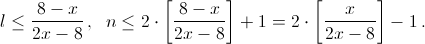 

  То есть в любом случае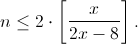  

  Покажем, что эта оценка достигается. Положим 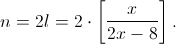    Рассмотрим все способы отметить l сотрудников из  n = 2l (число K таких способов равно  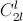 ).  Разобьём 8-часовой интервал на K отрезков длины ⁸/_K.  Каждому отрезку сопоставим группу из l человек; пусть в течение этого отрезка времени ровно эти l человек и находились в буфете. Из симметрии ясно, что для каждых двух сотрудников время, в течение которого ровно один из них был в буфете, одно и то же – пусть оно равно y. Тогда в подсчете, проделанном выше, все неравенства обратятся в равенства, и мы получим  8l² = (2l – 1)y.   Отсюда  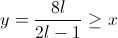   (последнее неравенство равносильно  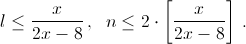  ),   что и требовалось.

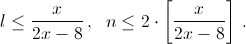  сотрудников.