Олимпиадная задача по топологии и алгебре: разбиение двузначных чисел, 9–11 класс

  Расположим все "двузначные" числа внутри квадратов решётки специального вида, как указано на рисунке.

  Назовём два квадрата этой решётки соседними, если их границы имеют общий отрезок. Тогда каждые два числа, расположенные в соседних квадратах, будут отличаться друг от друга на 1, 10 или 11.

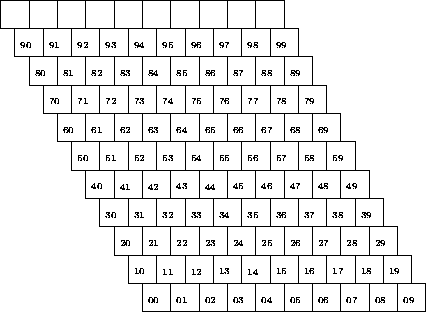
  Разобьём "двузначные" числа произвольным образом на две группы. Будем называть чёрными все квадраты верхней (незаполненной) строки, а также все такие квадраты S, для которых найдётся ломаная L(S) с началом в центре S и концом в центре какого-либо квадрата верхней строки, все звенья которой соединяют центры соседних квадратов, не содержащих числа второй группы. Остальные соседние с чёрными квадраты решётки будем называть белыми. Нетрудно видеть, что все белые квадраты содержат числа второй группы.

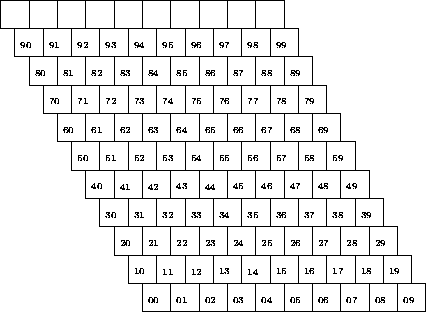
  Если в нижней строке решётки найдётся чёрный квадрат S , то следуя вдоль звеньев ломаной L(S) до её пересечения с верхней строкой, запишем в ряд числа первой группы, расположенные в квадратах, через которые эта ломаная проходит (см. рис.).

  Соседние числа этого ряда расположены в соседних квадратах и, следовательно, отличаются на 1, 10 или 11. Заметим также, что ломаная L(S) пересекает каждую строку решётки. Значит, в разряде десятков чисел построенного ряда встретятся все 10 различных цифр. В этом случае искомый ряд построен из чисел первой группы.

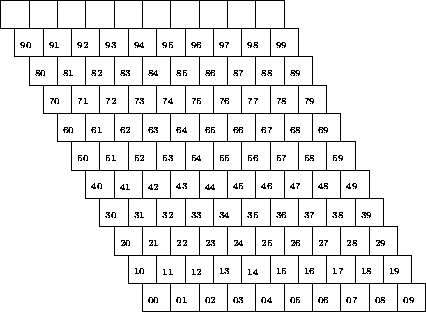
  Если же в нижней строке решётки нет чёрных квадратов, то рассмотрим фигуру, образованную чёрными квадратами (см. рис.).

  Внешний её периметр представляет собой замкнутую ломаную, все вершины которой являются вершинами квадратов решётки, а каждое из её звеньев принадлежит одному из двух типов: оно является либо отрезком внешней границы решётки, либо общим отрезком границ чёрного и белого квадратов. Некоторые звенья второго типа образуют ломаную l с началом в вершине левого края решётки и концом в вершине правого края решётки. Следуя вдоль звеньев ломаной l, запишем в ряд числа, расположенные в белых квадратах, вдоль границ которых мы проходим. Все эти числа принадлежат второй группе. Заметим, что если какие-либо два соседних звена ломаной l не являются частью границы одного белого квадрата, то два белых квадрата, вдоль границ которых они проходят, сами являются соседними. Следовательно, каждые два соседних числа построенного ряда отличаются на 1, 10 или 11. Квадраты первого и последнего чисел этого ряда примыкают соответственно к левому и правому краям решётки, поэтому ломаная l пересечёт каждый из наклонных влево столбов решётки. Следовательно, в разряде единиц чисел построенного ряда встретятся все 10 различных цифр. В этом случае искомый ряд построен из чисел второй группы.

  Отметим, что числа каждого из построенных в этих двух случаях рядов могут повторяться. Отбрасывая "зацикленные" участки такого ряда, можно получить искомый ряд уже без повторений входящих в него чисел.

Ответ задачи отсутствует