Олимпиадная задача: разбиение "лестницы" высоты n на уникальные прямоугольники
Задача
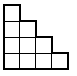 Назовём лестницей высоты n фигуру, состоящую из всех клеток квадрата n×n, лежащих не выше диагонали (на рисунке показана лестница высоты 4). Сколькими различными способами можно разбить лестницу высоты n на несколько прямоугольников, стороны которых идут по линиям сетки, а площади попарно различны?
Назовём лестницей высоты n фигуру, состоящую из всех клеток квадрата n×n, лежащих не выше диагонали (на рисунке показана лестница высоты 4). Сколькими различными способами можно разбить лестницу высоты n на несколько прямоугольников, стороны которых идут по линиям сетки, а площади попарно различны?
Решение
Отметим в каждом столбце лестницы по одной верхней клетке; назовём их объединение верхним слоем. Никакие две из n клеток этого слоя не могут лежать в одном прямоугольнике разбиения, поэтому в любом разбиении лестницы не менее n прямоугольников. С другой стороны, минимальная суммарная площадь n прямоугольников с различными площадями равна 1 + 2 + ... + n, что совпадает с площадью всей лестницы. Значит, число прямоугольников в любом разбиении равно n, их площади выражаются числами 1, 2, ..., n, и каждый из них содержит клетку верхнего слоя.
Покажем индукцией по n, что число требуемых разбиений лестницы высоты n равно 2n–1. База (n = 1) очевидна.
Шаг индукции. Рассмотрим разрезание лестницы высоты n на прямоугольники площади 1, 2, ..., n. Прямоугольник, покрывающий угловую (наиболее далекую от верхнего слоя) клетку лестницы, содержит клетку верхнего слоя, то есть сумма длин его сторон a и b равна n + 1. Поэтому его площадь ab > a + b – 1 = n (так как ab – (a + b – 1) = (a – 1)(b – 1) > 0); при этом равенство может достигаться лишь при a = 1 или b = 1. Значит, одна из сторон нашего прямоугольника равна 1, а другая – n. Такой прямоугольник можно выбрать двумя способами (вертикальный или горизонтальный), причем в обоих случаях после его отрезания остается лестница высоты n – 1, количество способов разрезать которую на оставшиеся прямоугольники равно 2n–2. Значит, искомое количество способов равно 2·2n–2 = 2n–1.
Ответ
2n–1 способами.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь