Олимпиадная задача Гальперина Г. А. по стереометрии для 10-11 класса: монеты и шары

Так как при растяжении в  R раз площади меняются в  R² , а объёмы в  R³ раз, площадь круга радиуса R равна V₂R² , а площадь шара V₃R³ , где V₂ и  V₃  — некоторые константы (площадь единичного круга и объём единичного шара, соответственно; на самом делеV₂=π , а V₃=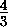π , но для решения задачи это не важно). Обозначим радиусы монет через R₁ , R₂ и  R₃ . Вначале весы были в равновесии, поэтомуV₂R₁²+V₂R₂²=V₂R₃² , т. е.

R₁²+R₂²=R₃².

Аналогично, чтобы определить, что произошло с весами, после того как монеты заменили шарами, нужно сравнитьR₁³+R₂³ с  R₃³ . Но по сравнению с равенством выше правая часть умножилась на больший радиус R₃ , а два слагаемых в левой части — на меньшие радиусы R₁ и  R₂ :

R₁³+R₂³= R₁²· R₁+R₂²· R₂< R₁²· R₃+R₂²· R₃= (R₁²+R₂²)· R₃= R₃³.

Значит, правая чаша перевесит.

Перевесит правая чаша весов.