Олимпиадная задача по планиметрии: доказательство о вписанных окружностях в треугольнике для 9–11 класса

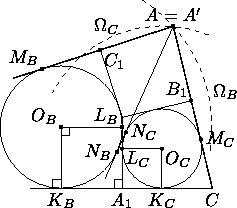
Пусть  ω_B касается  BA₁ , IA₁ и  BC₁ в точках  K_B , L_B и  M_B соответственно, а  ω_C касается  CA₁ , IA₁ и  CB₁ в точках  K_C , L_C и  M_C соответственно. Обозначим через  O_B и  O_C центры окружностей  ω_A и  ω_B соответственно, а через  r_B и  r_C  — их радиусы (пусть для определенностиr_B>r_C ). Тогда четырехугольники  O_BK_BA₁L_B и  O_CK_CA₁L_C  — квадраты, поэтому A₁L_B=r_B , A₁L_C=r_C и L_BL_C=r_B-r_C . Тогда, если вторая общая внутренняя касательная 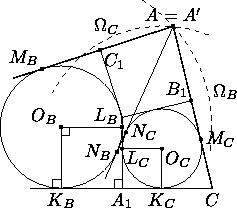 касается  ω_B и  ω_C в точках N_B и N_C , то N_BN_C=r_B-r_C , причем N_C и L_B лежат по одну сторону от линии центров  O_BO_C (заметим, что точка  A лежит по ту же сторону). Аналогично получаем, что C₁M_B=r_B , B₁M_C=r_C . Отложим на продолжении отрезка N_BN_C за точку N_C отрезок N_CA'=AM_C=AB₁+B₁M_C . Тогда N_BA'=AM_C+N_BN_C=(AB₁+r_C)+(r_B-r_C)=AC₁+r_B=AM_B . Итак, касательные из точек  A и  A' к окружности  ω_B равны, и касательные из них к  ω_C также равны. Заметим, что ГМТ, длина касательной из которых к окружности  ω_B равна  AM_B , есть окружность  Ω_B с центром  O_B и радиусом 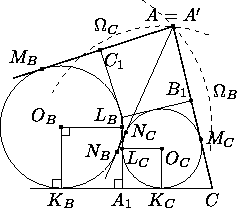 . Таким образом, точки  A и  A' лежат на  Ω_B . Аналогично, они лежат на окружности  Ω_C с центром  O_C и радиусом  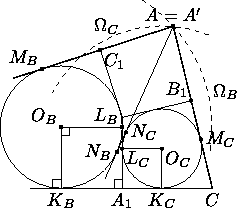. Итак, каждая из точек  A и  A' является одной из двух точек пересечения окружностей  Ω_B и  Ω_C , а поскольку A и A' лежат по одну сторону от  O_BO_C , имеем  A'=A . Значит, A лежит на прямой  N_BN_C , что и требовалось доказать.

Ответ задачи отсутствует