Олимпиадная задача по планиметрии для 8-9 класса: нахождение длин MO, MC, MH, MP
Задача
Точка M лежит вне окружности с центром O. Прямая OM пересекает окружность в точках A и B, прямая, проходящая через точку M, касается окружности в точке C, точка H – проекция точки C на AB, а перпендикуляр к AB, восставленный в точке O, пересекает окружность в точке P. Известно, что MA = a и MB = b. Найдите MO, MC, MH, MP и расположите найденные значения по возрастанию.
Решение
Для определённости будем считать, что a > b. Точка O – середина отрезка AB, поэтому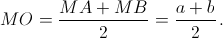 
По теореме о касательной и секущей
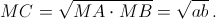
CH – высота прямоугольного треугольника OCM, проведённая из вершины прямого угла, поэтому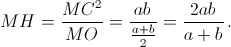 
По теореме Пифагора из прямоугольного треугольника MOP находим, что
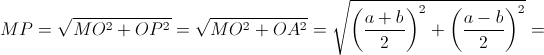
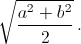
MH – катет прямоугольного треугольника MCH с гипотенузой MC, поэтому MH < MC.
MC – катет прямоугольного треугольника MOC с гипотенузой MO, поэтому MC < MO.
MO – катет прямоугольного треугольника MOP с гипотенузой MP, поэтому MO < MP.
Ответ
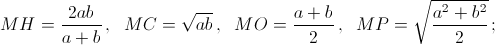MH < MC < MO < MP.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь