Олимпиадная задача по планиметрии: проекции и равнобедренная трапеция для 8-9 классов
Задача
Окружность вписана в равнобедренную трапецию ABCD с основаниями BC = a и AD = b. Точка H – проекция вершины B на AD, точка P – проекция точки H на AB, точка F лежит на отрезке BH, причём FH = AH. Найдите AB, BH, BP, DF и расположите найденные величины по возрастанию.
Решение
Для определённости будем считать, что a < b.
Если в четырёхугольник вписана окружность, то суммы его противоположных сторон равны, поэтому AB + CD = BC + AD = a + b, а так как
AB = CD, то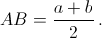 
Пусть O – центр окружности радиуса r, вписанной в трапецию ABCD, M – точка касания окружности с боковой стороной AB. Тогда BM = ½ BC = a/2,
AM = ½ AD = b/2. Отрезок OM – высота прямоугольного треугольника AOB, проведённая из вершины прямого угла, поэтому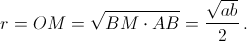 
Следовательно,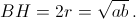 
Отрезок HP – высота прямоугольного треугольника AHB, проведённая из вершины прямого угла, поэтому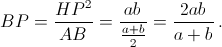 
Поскольку трапеция ABCD равнобедренная,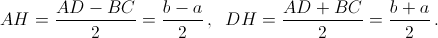 
Из прямоугольного треугольника DFH по теореме Пифагора находим,
что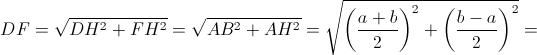 
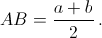
BP – катет прямоугольного треугольника BPH с гипотенузой BH, поэтому BP < BH.
BH – катет прямоугольного треугольника ABH с гипотенузой AB, поэтому BH < AB.
DH – катет прямоугольного треугольника DFH с гипотенузой DF, поэтому AB = DH < DF.
Ответ
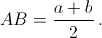BP < BH < AB < DF.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь