Назад

Олимпиадная задача по планиметрии: перпендикулярность прямых AB и PQ для 8-10 классов

Задача 215730 • Сложность: 2 • 8-10 класс
Задача

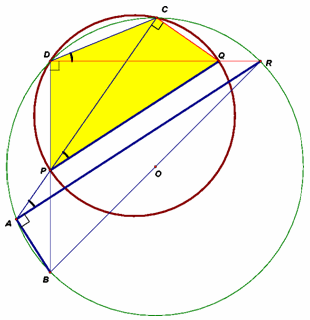
Хорды AC и BD окружности пересекаются в точке P. Перпендикуляры к AC и BD в точках C и D, соответственно пересекаются в точке Q .

Докажите, что прямые AB и PQ перпендикулярны.

Авторы:
Заславский А. А.
Разделы:
Планиметрия
Источники:
I Олимпиада по геометрии имени И.Ф. Шарыгина (2005 г.) Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина Заочный тур
Количество версий:
5
Решение

  Пусть указанные перпендикуляры пересекаются внутри окружности (случай внешней точки рассматривается аналогично). Отметим точку R – вторую точку пересечения прямой DQ с окружностью (см. рис.).

  ТочкиCиDлежат на окружности с диаметромPQ, поэтому  ∠CDQ= ∠CPQ.  Аналогично  ∠CDQ= ∠CAR= ∠CAR,  и, значит, прямыеPQиARпараллельны (соответственные углы равны). НоBRявляется диаметром, как следует из условия, поэтому  ∠BAR= 90°.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет