Назад

Олимпиадная задача по планиметрии: геометрическое место точек в треугольнике ABC

Задача 215734 • Сложность: 3 • 8-9 класс
Задача

Имеются две параллельные прямые p1 и p2. Точки A и B лежат на p1, а C – на p2. Будем перемещать отрезок BC параллельно самому себе и рассмотрим все треугольники ABC, полученные таким образом. Найдите геометрическое место точек, являющихся в этих треугольниках:

  а) точками пересечения высот;

  б) точками пересечения медиан;

  в) центрами описанных окружностей.

Авторы:
Мякишев А. Г.
Разделы:
Планиметрия
Источники:
I Олимпиада по геометрии имени И.Ф. Шарыгина (2005 г.) Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина Заочный тур
Количество версий:
5
Решение

  а) Очевидно, получается прямая, перпендикулярная BC и проходящая через вершину A.

  б) Ответом будет прямая, параллельная данным прямым и делящая отрезок с концами на этих прямых в отношении  1 : 2,  считая от p1 (рис. справа). В самом деле, если отрезок BC движется с постоянной скоростью, то и его середина движется с постоянной скоростью. Точка пересечения медиан делит отрезок, соединяющий вершину А с серединой ВС, в постоянном отношении  2 : 1  и, следовательно, также будет двигаться с постоянной скоростью по указанной прямой.   в) Первый способ. Серединные перпендикуляры к отрезкам AB и BC также движутся с постоянными скоростями. Значит, и точка их пересечения (центр описанной окружности) будет перемещаться по прямой (рис. слева).
  Второй способ. Рассмотрим отрезок AC0 (в который вырождается треугольник при совпадении точек A и B) и симметричный ему относительно перпендикуляра, опущенного на p2 из точки A, отрезок AK. Тогда ABCK – равнобокая трапеция, следовательно, точка K лежит на описанной окружности треугольника ABC (рис. справа). Значит, точка O лежит на серединном перпендикуляром к отрезку AK.
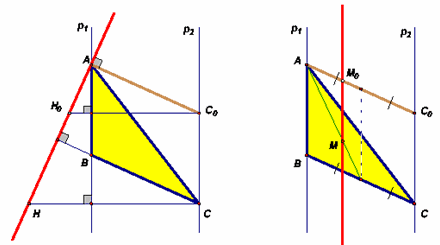
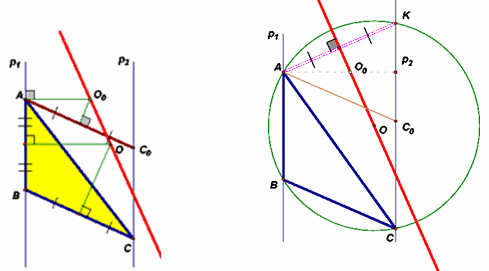
Ответ

Во всех случаях получится прямая с выколотой точкой, которая соответствует случаю, когда треугольник вырождается в отрезок.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет