Олимпиадная задача по планиметрии: равенство углов в треугольнике с биссектрисой для 8–11 классов
Задача
В треугольнике ABC провели биссектрису CL. Точки A1 и B1 симметричны точкам A и B относительно прямой CL, A2 и B2 симметричны точкам A и B относительно точки L. Пусть O1 и O2 – центры описанных окружностей треугольников AB1B2 и BA1A2. Докажите, что углы O1CA и O2CB равны.
Решение
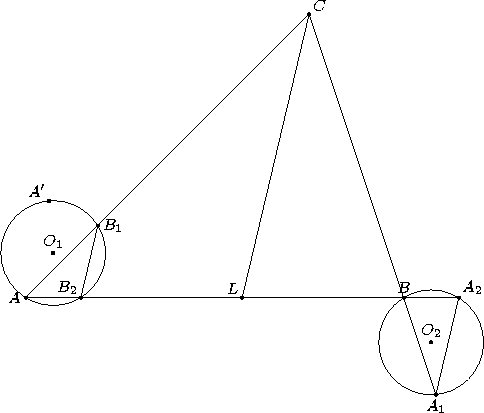
Из условия следует, что CB1 : CA = CB : CA = BL : LA = B2L : AL, то есть B1B2 || CL (см. рис.). Аналогично A1A2 || CL. Значит,
∠AB1B2 = ∠BA1A2 = ½ ∠C. При симметрии относительно CL точки B и A1 перейдут в B1 и A, а точка A2 – в некоторую точку A'. При этом
∠A'AB2 + ∠ A'B1B2 = ∠A + ∠B + 2·½ ∠C = 180°. Следовательно, четырёхугольник AA'B1B2 – вписанный и точки O1, O2 симметричны относительно CL.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь