Олимпиадная задача по стереометрии: геометрическое место точек пересечения медиан
Задача
Дан трёхгранный угол с вершиной O и точка A на его ребре. По двум другим его рёбрам скользят точки B и C . Найдите геометрическое место точек пересечения медиан треугольников ABC .
Решение
Пусть B и C — произвольные точки на рёбрах
данного трёхгранного угла OABC , K — середина
отрезка BC , M — точка пересечения медиан
треугольника ABC . Тогда 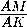 =
=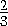 .
При гомотетии с центром A и коэффициентом
.
При гомотетии с центром A и коэффициентом 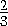 точка K перейдёт в точку M , плоскость OBC —
в плоскость α , проходящую через точку M параллельно
грани OBC , а грань OBC — в пересечение плоскости α с данным трёхгранным углом. Следовательно, каждая такая точка M принадлежит этому пересечению.
Пусть теперь M — произвольная точка построенного пересечения.
При гомотетии с центром A и коэффициентом
точка K перейдёт в точку M , плоскость OBC —
в плоскость α , проходящую через точку M параллельно
грани OBC , а грань OBC — в пересечение плоскости α с данным трёхгранным углом. Следовательно, каждая такая точка M принадлежит этому пересечению.
Пусть теперь M — произвольная точка построенного пересечения.
При гомотетии с центром A и коэффициентом 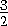 это
пересечение перейдёт в грань, противоположную ребру OA , а точка M — в некоторую точку K , лежащую в этой грани. Известно, что для
любой точки K , лежащей внутри угла, найдётся отрезок BC с концами
на сторонах угла, для которого точка K будет серединой. При этом
это
пересечение перейдёт в грань, противоположную ребру OA , а точка M — в некоторую точку K , лежащую в этой грани. Известно, что для
любой точки K , лежащей внутри угла, найдётся отрезок BC с концами
на сторонах угла, для которого точка K будет серединой. При этом 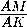 =
=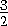 . Следовательно, M — точка пересечения
медиан треугольника ABC . Что и требовалось доказать.
. Следовательно, M — точка пересечения
медиан треугольника ABC . Что и требовалось доказать.
Ответ
Рассмотрим плоскость, параллельную грани OBC и отстоящую от неё на треть расстояния между точкой A и гранью OBC . Искомое ГМТ — часть этой плоскости, лежащая внутри данного трёхгранного угла.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь