Олимпиадная задача по стереометрии: тетраэдр, расстояния и середины рёбер

Докажем сначала, что сумма квадратов расстояний от произвольной точки пространства до двух противоположных вершин прямоугольника равна сумме квадратов расстояний от этой точки до двух других его вершин. Действительно, пусть KLMN — прямоугольник со сторонами KL=a и KN=b (рис.1). Выберем прямоугольную систему координат, направив ось OX по лучу KL , ось OY — по лучу KN , а ось OZ по лучу с началом в точке K и перпендикулярному плоскости прямоугольника. Пусть P(x;y;z)— произвольная точка пространства. Найдём квадраты расстояний от этой точки до вершин K(0;0;0), L(a;0;0), M(a;b;0)и N(0;b;0):

PK2 = (x-0)2+(y-0)2+(z-0)2 = x2+y2+z2,

PL2 = (x-a)2+(y-0)2+(z-0)2 = (x-a)2+y2+z2,

PM2 = (x-a)2+(y-b)2+(z-0)2 = (x-a)2+(y-b)2+z2,

PN2 = (x-0)2+(y-b)2+(z-0)2 = x2+(y-b)2+z2.

Следовательно,

PK2 +PM2 = (x2+y2+z2)+ ((x-a)2+(y-b)2+z2)=

=((x-a)2+y2+z2) + (x2+(y-b)2+z2) = PL2+PN2.

Что и требовалось доказать. Перейдём к нашей задаче (рис.2). Пусть K , L , M и N — середины рёбер AC , AD , BD и BC соответственно. Тогда ML и KN — средние линии треугольников ABD и ABC , поэтому ML=AB=KN и ML || AB || KN , значит, четырёхугольник KLMN — параллелограмм, а т.к. KL || CD , KN || AB и AB 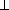CD , то это прямоугольник. Тогда по доказанному утверждению PM2+PK2=PL2+PN2. Что и требовалось доказать.

Ответ задачи отсутствует