Олимпиадная задача по стереометрии для 10–11 класса: высоты тетраэдра пересекаются

Докажем сначала следующее утверждение. Если противоположные рёбра тетраэдра попарно перпендикулярны, то все высоты тетраэдра (или их продолжения) пересекаются в одной точке. Действительно, пусть в тетраэдре ABCD известно, что AB 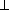CD , AC 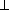BD и BC 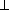AD , а DD1— высота тетраэдра (рис.1). Тогда прямая CD1— ортогональная проекция наклонной CD к плоскости основания ABC , а т.к. CD 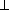AB , то по теореме о трёх перпендикулярах CD1 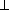AB . Аналогично, AD1 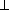BC , значит, D1— точка пересечения высот треугольника ABC . Аналогично докажем, что остальные высоты тетраэдра также проходят через точки пересечения высот граней тетраэдра. Пусть AA1— высота тетраэдра, а плоскость, проведённая через пересекающиеся прямые AD и DD1, пересекает прямую BC в точке M . Тогда AM — высота треугольника ABC , а DM — высота треугольника BDC (теорема о трёх перпендикулярах), значит, прямая DM проходит через точку пересечения высот треугольника BDC , т.е. через точку A1. Поэтому прямые AA1и DD1лежат в одной плоскости, и значит, пересекаются. Аналогично докажем, что две любые высоты тетраэдра ABCD пересекаются. При этом все четыре высоты не лежат в одной плоскости, иначе в одной плоскости лежали бы точки A , B , C и D . Следовательно, прямые AA1, BB1, CC1и DD1пересекаются в одной точке. Перейдём к нашей задаче (рис.2). Пусть высота DD1тетраэдра ABCD пересекается с высотами AA1и BB1, а плоскость, проведённая через пересекающиеся прямые DD1и AA1, пересекает прямую BC в точке M . Тогда по теореме о трёх перпендикулярах AM 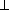BC , т.е. AM — высота треугольника ABC . Аналогично докажем, что если плоскость, проведённая через пересекающиеся прямые DD1и BB1, пересекает прямую AC в точке N , то BN — также высота треугольника ABC , а т.к. прямые AM и BN пересекаются в точке D1, то D1— точка пересечения высот треугольника ABC . Тогда по теореме о трёх перпендикулярах противоположные рёбра тетраэдра попарно перпендикулярны. Из доказанного ранее утверждения следует, что все высоты тетраэдра пересекаются в одной точке.

Ответ задачи отсутствует