Олимпиадная задача по планиметрии: угол между медианами в треугольнике

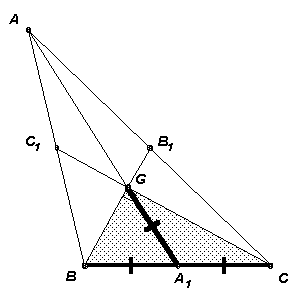
  Пусть АА₁, BB₁ и СС₁ – медианы треугольника АВС, пересекающиеся в точке G, и  АА₁ = 1,5ВС  (см. рис.).

  Тогда  GA₁ = ¹/₃ AA₁ = ½ ВС,  то есть медиана GA треугольника BGC₁ равна половине стороны ВС, к которой она проведена. Следовательно, этот треугольник – прямоугольный.

90°.