Олимпиадная задача по планиметрии: площадь четырёхугольника KBLM в правильном шестиугольнике
Задача
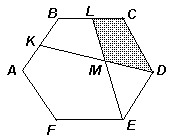
Точки K и L – середины сторон АВ и ВС правильного шестиугольника АВСDEF. Отрезки KD и LE пересекаются в точке М. Площадь треугольника DEM равна 12. Найдите площадь четырёхугольника KBLM.
Решение
Так как четырёхугольник KBCD является образом четырёхугольника LCDE при повороте вокруг центра АВСDEF на угол 60°, то эти четырёхугольники равны, а значит, и равновелики (см. рис.). Вычитая из площади каждого из них площадь четырёхугольника LCDM, получим, что SKBLM = SDEM = 12.
Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет