Олимпиадная задача по планиметрии: основания трапеции и острый угол (9-11 класс)

  Пусть ABCD – данная трапеция с основаниями  BC = 2  и  AD = 11  (см. рис.). Проведём  CM || BA,  тогда угол между продолжениями боковых сторон трапеции равен углу DCM. Пусть  CM = AB = x,  тогда  DC = 13 – x  (так как ABCD – описанная трапеция).

  В треугольнике DCM  MD² = (AD – BC)² = 81,  CM² + CD² = x² + (13 – x)².  Так как  CM² + CD² – MD² = 2x² – 26x + 88 = 2(x – 6,5)² + 1,75 > 0,  то

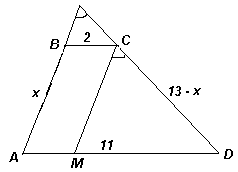
CM² + CD² > MD²,  значит, угол DCM – острый.

Ответ задачи отсутствует