Олимпиадная задача по планиметрии: сравнение углов в равнобокой трапеции
Задача
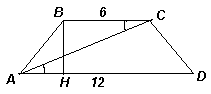
В равнобокой трапеции AВСD основания AD и ВС равны 12 и 6 соответственно, а высота равна 4. Сравните углы ВАС и САD.
Решение
Так как AD || BC, то ∠CAD = ∠BCA (см. рис.). Пусть BH – высота трапеции. Тогда AH = ½ (AD – BC) = 3; BH = 4, и из прямоугольного треугольника АВН находим, что AB = 5.
Таким образом, в треугольнике АBC BC > AB, значит, ∠BAC > ∠BCA (против большей стороны треугольника лежит больший угол). Следовательно, ∠BAC > ∠CAD.
Ответ
∠ВАС > ∠CAD.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет