Олимпиадная задача по стереометрии: пирамида и цилиндр, 10–11 класс, Кожевников П. А.
Задача
Bсе ребра правильной четырехугольной пирамиды равны 1, а все вершины лежат на боковой поверхности (бесконечного) прямого кругового цилиндра радиуса R. Найдите все возможные значения R.
Решение
Пусть SABCD – данная пирамида (ABCD –
единичный квадрат с центром O). Cразу заметим, что O удалена
от всех вершин пирамиды на расстояние 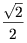 (рассмотрев точку
S', симметричную S относительно O, пирамиду можно достроить
до правильного октаэдра с вершинами A, B, C, D, S, S' и центром
O). Пусть вершины пирамиды лежат на цилиндре радиуса R с осью
l; w – круговое сечение цилиндра (w имеет радиус R), проходящее
через S. Рассмотрим A', B', C', D' – точки на окружности
w, являющиеся проекциями точек A, B, C, D на плоскость
окружности w. Пусть AB не параллельна l, то есть A' ≠ B'. Так
как
(рассмотрев точку
S', симметричную S относительно O, пирамиду можно достроить
до правильного октаэдра с вершинами A, B, C, D, S, S' и центром
O). Пусть вершины пирамиды лежат на цилиндре радиуса R с осью
l; w – круговое сечение цилиндра (w имеет радиус R), проходящее
через S. Рассмотрим A', B', C', D' – точки на окружности
w, являющиеся проекциями точек A, B, C, D на плоскость
окружности w. Пусть AB не параллельна l, то есть A' ≠ B'. Так
как 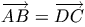 , то
, то 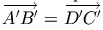 ,
значит либо A' = D' и B' = C', либо
A'B'C'D' – прямоугольник, вписанный в окружность w.
Рассмотрим отдельно эти два
случая.1) Если A' = D' и B' = C', то ребра AD и BC параллельны l, а значит A'B'S – сечение
пирамиды, проведенное через S перпендикулярно AD (см. рис. а). Тогда
A' и B' – середины ребер
AD и BC, A'B' = AB = 1, O – середина A'B',
SA' и SB' – высоты граней SAD, SBC, то есть
,
значит либо A' = D' и B' = C', либо
A'B'C'D' – прямоугольник, вписанный в окружность w.
Рассмотрим отдельно эти два
случая.1) Если A' = D' и B' = C', то ребра AD и BC параллельны l, а значит A'B'S – сечение
пирамиды, проведенное через S перпендикулярно AD (см. рис. а). Тогда
A' и B' – середины ребер
AD и BC, A'B' = AB = 1, O – середина A'B',
SA' и SB' – высоты граней SAD, SBC, то есть
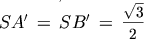 . Находим
. Находим 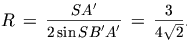 .
Наоборот, если описать вокруг серединного сечения
SA'B' пирамиды окружность w и взять прямой круговой цилиндр с направляющей w, то
AD и BC будут образующими цилиндра, то есть рассматриваемая выше конструкция
возможна.
.
Наоборот, если описать вокруг серединного сечения
SA'B' пирамиды окружность w и взять прямой круговой цилиндр с направляющей w, то
AD и BC будут образующими цилиндра, то есть рассматриваемая выше конструкция
возможна.
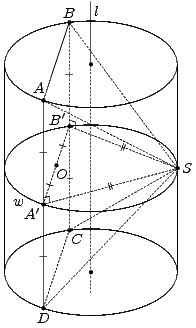 |  | |
| Рис. а | Рис. б |
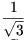 .
Наоборот, в правильном октаэдре с вершинами A, B, C, D,
S, S' окружности w и w', описанные около правильных
треугольников ABS и CDS', лежат на описанной вокруг
октаэдра сфере и симметричны относительно центра сферы O,
поэтому w и w' принадлежат одному круговому цилиндру,
то есть рассматриваемая во втором случае конструкция
возможна.
.
Наоборот, в правильном октаэдре с вершинами A, B, C, D,
S, S' окружности w и w', описанные около правильных
треугольников ABS и CDS', лежат на описанной вокруг
октаэдра сфере и симметричны относительно центра сферы O,
поэтому w и w' принадлежат одному круговому цилиндру,
то есть рассматриваемая во втором случае конструкция
возможна.
Ответ
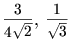 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь