Олимпиадная задача по планиметрии: площади трапеции и параллелограмма (10-11 класс)
Задача
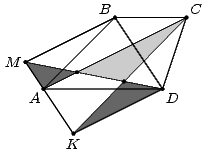
Трапеция ABCD и параллелограмм MBDK расположены так, что стороны параллелограмма параллельны диагоналям трапеции (см. рис.). Докажите, что площадь серой части равна сумме площадей черных частей.
Решение
Заметим, что утверждение задачи равносильно равенству площадей треугольников KMD и AKC (см. рис.). Так как AC || KD, то AKDC — трапеция, следовательно, SAKC = SADC. Аналогично, в трапеции ABCD: SADC = SADB. В то же время, SADB = 1/2SMBDK = SKMD. Что и требовалось.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет