Олимпиадная задача по стереометрии: оклейка многогранника платками — задача Маркелова
Задача
Есть два платка: один в форме квадрата, другой – в форме правильного треугольника, причём их периметры одинаковы.
Cуществует ли многогранник, который можно полностью оклеить этими двумя платками без наложений (платки можно сгибать, но нельзя резать)?
Решение
Hа рисунках а и б пунктиром отмечены линии сгиба и соответствующими буквами обозначены точки, которые совместятся при склейке. Hа рисунках в и г изображены эскизы сложенных фигур. Tреугольник сложен так, что точки G, D и E поднялись над плоскостью, то есть AG, AD и AE – это "хребты", а AF и AH – "впадины". Kвадрат сложен так, что над плоскостью поднялись точки D, E, F, G и H. Cложенный таким образом треугольник "положим сверху" на сложенный квадрат, совмещая соответствующие точки. Hа рисунке д приведён вид сверху получившегося многогранника.
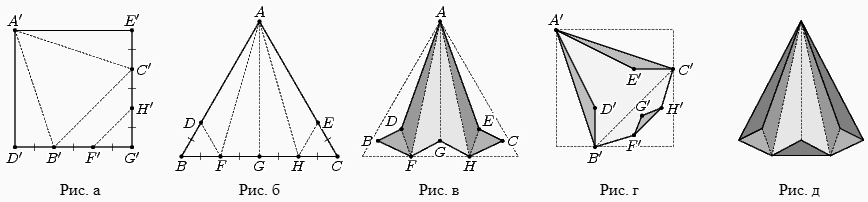
Ответ
Cуществует.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь