Олимпиадная задача по планиметрии для 8–9 классов от Блинкова Ю. А.

Решение 1:   Докажем, что точки K и M лежат на серединном перпендикуляре к отрезку A₁B₁.

  M – середина AB, значит,  AM = MB₁ = MA₁. Так как равные хорды стягивают равные дуги, то KM – биссектриса угла AKA₁. Также ∠KB₁M = 180° – ∠AB ₁M = 180° – ∠B₁AM = ∠KA₁M.  Значит, треугольники KB₁M и KA₁M равны, и  KB₁ = KA₁,  что и требовалось.   Для точки L доказательство аналогично.

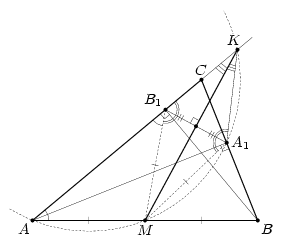
Решение 2:   Поскольку M – центр окружности, описанной вокруг четырёхугольника BA₁B₁A, то  ∠MB₁B = ∠MBB₁ = ∠AA₁B₁  и  ∠MAA₁ = ∠MA₁A.  Поскольку четырёхугольник MAKA₁ – вписанный, то  ∠A₁MK = ∠A₁AK.  Следовательно,  ∠MA₁A + ∠AA₁B₁ + ∠A₁MK = ∠MAA₁ + ∠ABB₁ + ∠A₁AB₁ = 90°.  Из этого следует, что  A₁B₁ ⊥ MK.

  Аналогично доказывается, что  A₁B₁ ⊥ ML.  Значит, прямые MK и ML совпадают.

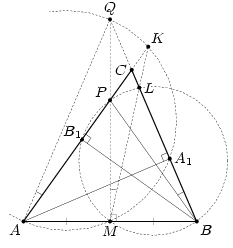
Решение 3:   Пусть прямые AC и BCпересекают серединный перпендикуляр к AB в точках P и Q соответственно.

  ТогдаAQ– диаметр описанной окружности треугольникаAMA₁. AналогичноBP– диаметр описанной окружности треугольникаBMB₁.   Используя свойство вписанных углов и то, что треугольникиABQиABPравнобедренные, получим ∠QMK= ∠QAK= ∠QBP= ∠PBL= ∠PML, откуда и следует утверждение задачи.

Ответ задачи отсутствует