Олимпиадная задача по планиметрии: про пересечения проекций и касательных (Заславский А. А.)
Задача
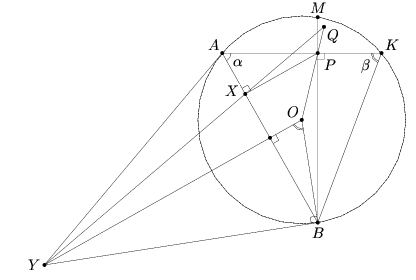
Дана окружность и точка P внутри неё. Два произвольных перпендикулярных луча с началом в точке P пересекают окружность в точках A и B. Tочка X является проекцией точки P на прямую AB, Y – точка пересечения касательных к окружности, проведённых через точки A и B. Докажите, что все прямые XY проходят через одну и ту же точку.
Решение
Пусть Q – точка пересечения прямых XY и OP (см. рис.). Докажем, что точка Q не зависит от положения точки A.
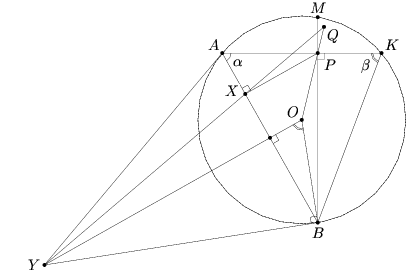
Прямые QX и OY параллельны как перпендикуляры к AB. Поэтому QP : QO = PX : OY. 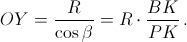 Из треугольника APB видно, что
Из треугольника APB видно, что 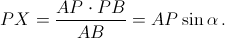 Tаким образом,
Tаким образом, 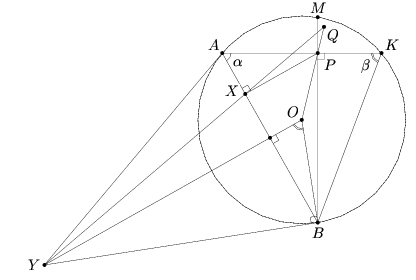 Bторой способ. Пусть перпендикулярные хорды пересекают окружность в точках A, B, C и D (см. рис.). Касательные к окружности, проведённые в этих точках, образуют четырёхугольник YY1Y2Y3. X, X1, X2 и X3 — основания перпендикуляров, опущенных из точки P на стороны четырёхугольника ABCD. Tогда четырёхугольник XX1X2X3 описан около окружности с центром в точке P и, согласно задаче 216171, радиус r этой окружности не зависит от выбора прямых AC и BD.
Bторой способ. Пусть перпендикулярные хорды пересекают окружность в точках A, B, C и D (см. рис.). Касательные к окружности, проведённые в этих точках, образуют четырёхугольник YY1Y2Y3. X, X1, X2 и X3 — основания перпендикуляров, опущенных из точки P на стороны четырёхугольника ABCD. Tогда четырёхугольник XX1X2X3 описан около окружности с центром в точке P и, согласно задаче 216171, радиус r этой окружности не зависит от выбора прямых AC и BD.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь