Назад

Олимпиадная задача по планиметрии: угол PKА и угол QKD в трапеции для 9-10 классов

Задача 216218 • Сложность: 2 • 9-10 класс
Задача

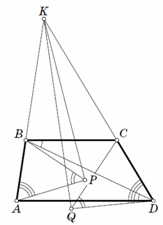
В трапеции ABCD с основаниями AD и BC лучи AB и DC пересекаются в точке K. Точки P и Q – центры описанных окружностей треугольников ABD и BCD. Докажите, что  ∠PKA = ∠QKD.

Авторы:
Акопян А. В.
Разделы:
Планиметрия
Источники:
Московская математическая олимпиада Олимпиады и турниры 2011 год
Количество версий:
5
Решение

Заметим, что  ∠ADB = ∠DBC  (см. рис.). С другой стороны,  ∠APB = 2∠ADB.  Аналогично  ∠DQC = 2∠DBC, а значит,   ∠APB = ∠DQC.

Следовательно, равнобедренные треугольникиAPBиDQCподобны. Поэтому  ∠KAP= ∠KDQ  и  AP:DQ = AB:DC.  Вместе с тем из теоремы о пропорциональных отрезках  AK:DK = AB:DC,  поэтому треугольникиAPKиDQKподобны по двум сторонам и углу между ними. Значит, ∠PKA= ∠QKD.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет