Олимпиадная задача Бородина П. А. по планиметрии для 9–11 классов: доказательство неравенства в равнобедренном треугольнике
Задача
В равнобедренном треугольнике ABC на основании BC взята точка D, а на боковой стороне AB – точки E и M так, что AM = ME и отрезок DM параллелен стороне AC. Докажите, что AD + DE > AB + BE.
Решение
Так как DM || AC, то ∠MDB = ∠C = ∠B и DM = MB = ME + EB. Обозначим через K середину отрезка DE (см. рис.). Тогда MK – средняя линия в треугольнике ADE и AD = 2MK. По неравенству треугольника AD + DE = 2(DK + KM) > 2MD = 2ME + 2EB = AE + EB + EB = AB + EB.
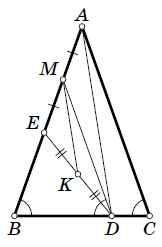
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет