Назад

Олимпиадная задача Бородина: размещение карточек с примерами и конструкциями в 11 классе

Задача 216233 • Сложность: 2 • 11 класс
Задача

Верно ли, что любые 100 карточек, на которых написано по одной цифре 1, 2 или 3, встречающейся не более чем по 50 раз каждая, можно разложить в один ряд так, чтобы в нём не было фрагментов 11, 22, 33, 123 и 321?

Авторы:
Бородин П. А.
Разделы:
Примеры и контрпримеры. Конструкции
Источники:
Московская математическая олимпиада Олимпиады и турниры 2011 год
Количество версий:
4
Решение

Пусть имеется x карточек с цифрой 1, y карточек с цифрой 2 и z карточек с цифрой 3. Тогда x + y + z = 100, и так как

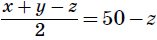то искомый ряд можно сложить изфрагментов 21, затем из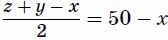фрагментов 32, а затем из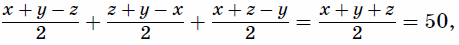фрагментов 31. При этом карточка с цифрой 1 встретится ровно
раз, карточка с цифрой 2 — ровноyраз, а карточка с цифрой 3 — ровноzраз, причём запрещённые фрагменты в предложенном ряде не встретятся, даже если какое-либо из значенийx,yилиzравно 50.
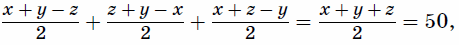
Ответ

верно.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет