Олимпиадная задача о трёх спортсменах, тренере и минимизации пути (8-9 класс)

  Присвоим номера спортсменам по убыванию их скоростей на старте. Нарисуем графики их движения, откладывая время по оси абсцисс, а расстояние до точки A – по оси ординат. Пусть O – начало координат, S – точка на оси ординат сооответствующая точке B,   (OS = 60 м),  K, L, M – точки на графиках трёх спортсменов в момент их нахождения в точке B, T – точка на оси абсцисс, соответствующая моменту финиша, P, Q, R – точки, соответствующие моменту встречи первого и второго, второго и третьего, третьего и первого спортсменов соответственно, P', Q' и R' – проекции этих точек на ось ординат (см. рис.).

  Заметим, что для любых трёх заданных точек на прямой существует единственная точка, сумма расстояний от которой до заданных будет минимальной – это средняя из трёх заданных точек. Следовательно, тренер всегда будет находиться рядом со спортсменом, который находился между двумя другими. Тогда график движения тренера описывается ломанойOPRQT, а длинаlего пути равна  OP' + P'R' + R'Q' + Q'O.   Обозначим длины отрезков KL, LM и OT через a, b и t соответственно. Так как  KL || OT,  то треугольники KPL и TPO подобны и

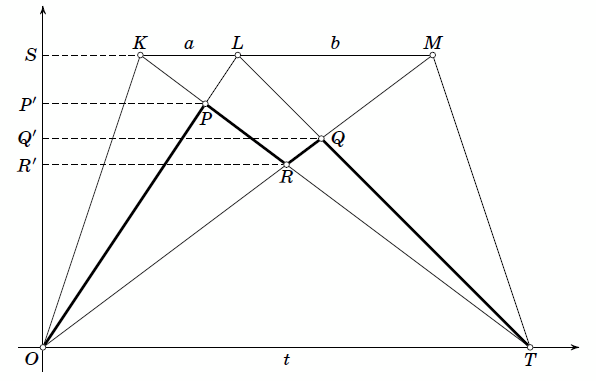
KP : PT = KL : OT = a : t.  Аналогично  LQ : QT = LM : OT = b : t  и  KR : RT = KM : OT = (a + b) : t.  По теореме о пропорциональных отрезках

SP' : P'O = KP : PT = a : t.  Отсюда  OP' = ^60t/_a+t.  Аналогично  OQ' = ^60t/_b+t  и  OR' = ^60t/_a+b+t.  Значит, 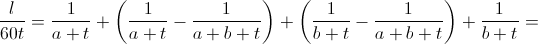 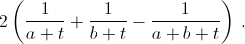 Так как  b < t – a,  а выражение 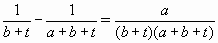    тем меньше, чем больше b, то  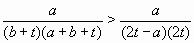  и

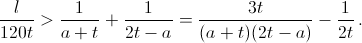
  Квадратный трёхчлен  (a + t)(2t – a)  (как функция от a) принимает наибольшее значение  ^9t²/₄  при  a = ^t/₂.  Значит,  l > 120t (⁴/_3t – ¹/_2t) = 100.

Не мог.