Олимпиадная задача по математике: найдите a > 1 для уравнения $a^x = \log_a x$

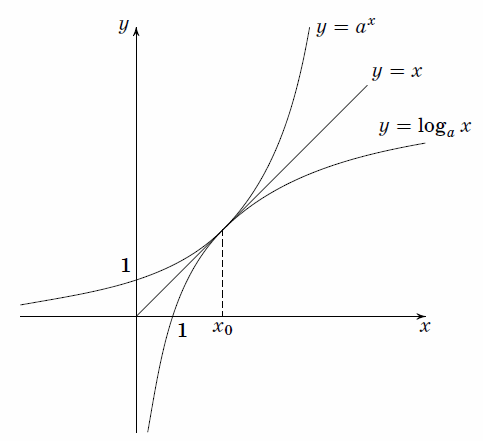
Рассмотрим графики функций $y = a^x$,  $y = \log_a x$  (см. рис.). Поскольку эти функции взаимно обратны, каждая их общая точка либо лежит на прямой $y=x$, либо симметрична другой их общей точке относительно этой прямой. Но при $a > 1$ обе эти функции возрастают, поэтому точки $(x_0,y_0)$ и $(y_0,x_0)$ могут быть общими только при $x_0=y_0$. Следовательно, уравнение $a^x = \log_a x$ эквивалентно уравнению $a^x = x$.

Ввиду очевидной выпуклости функции $f(x) = a^x$ последнее уравнение имеет единственное решение тогда и только тогда, когда график $y = a^x$ касается прямой $y = x$. Это значит, что в какой-то точке $x_0$ справедливо $f(x_0) = x_0$ и $f'(x_0) = a^{x_0} \ln a = 1$.  Отсюда $x_0 = \frac{1}{\ln a}$, то есть $e = a^{1/\ln a}=\frac{1}{\ln a}$, $\ln a = \frac{1}{e}$, $a=e^{1/e}$.

$a=e^{1/e}$.