Олимпиадная задача по стереометрии: тетраэдр ABCD, 10–11 класс, сложность 3/5
Задача
В пространстве даны точки A(-1;2;0), B(5;2;-1), C(2;-1;4)и D(-2;2;-1). Найдите: а) расстояние от вершины D тетраэдра ABCD до точки пересечения медиан основания ABC ; б) уравнение плоскости ABC ; в) высоту тетраэдра, проведённую из вершины D ; г) угол между прямыми BD и AC ; д) угол между гранями ABC и ACD ; е) расстояние между прямыми BD и AC .
Решение
а) Координаты точки M пересечения медиан треугольника ABC равны средним арифметичеким координат вершин
треугольника, т.е. xo=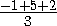 =2, yo=
=2, yo=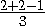 =1, zo=
=1, zo= =1.
Следовательно
=1.
Следовательно
DM=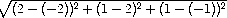 =
=
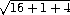 =
= 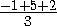 .
.
б) Найдём координаты векторов:
 =(5-(-1));2-2;-1-0)=(6;0;-1),
=(5-(-1));2-2;-1-0)=(6;0;-1),
 =(2-(-1));-1-2;4-0)=(3;-3;4).
=(2-(-1));-1-2;4-0)=(3;-3;4).
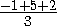 (a;b;c)— ненулевой вектор,
перпендикулярный плоскости ABC (вектор нормали).
Тогда
(a;b;c)— ненулевой вектор,
перпендикулярный плоскости ABC (вектор нормали).
Тогда  ·
· 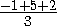 =0и
=0и  ·
· 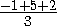 =0, или
=0, или
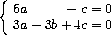
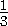 (3a+4c)=9.
Уравнение плоскости по точке A(-1;2;0)и вектору нормали
(3a+4c)=9.
Уравнение плоскости по точке A(-1;2;0)и вектору нормали 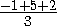 (a;b;c)имеет вид
(a;b;c)имеет вид
a(x+1)+b(y-2)+c(z-0)=0 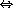 1(x+1)+9(y-2)+6(z-0)=0
1(x+1)+9(y-2)+6(z-0)=0  x+9y+6z-17=0.
x+9y+6z-17=0.
в) Высоту DH пирамиды ABCD найдём по формуле расстояния от точки до плоскости:
DH = 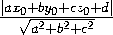 =
=
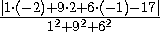 =
=
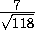 .
.
г) Угол между прямыми BD и AC равен либо углу между
векторами 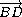 =(-2-5; 2-2;-1-(-1))=
(-7;0;0)и
=(-2-5; 2-2;-1-(-1))=
(-7;0;0)и  =(3;-3;4),
либо дополняет этот угол до180o , поэтому
=(3;-3;4),
либо дополняет этот угол до180o , поэтому
cos α = 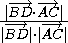 =
=
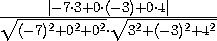 =
=
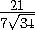 =
=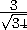 .
.
д) Пусть 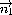 =(a1;b1;c1)—
вектор нормали плоскости ACD . Тогда
=(a1;b1;c1)—
вектор нормали плоскости ACD . Тогда 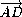 ·
· 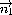 =0и
=0и  ·
· 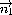 =0, где
=0, где 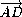 =(-2-(-1);2-2;-1-0)=(-1;0;-1)и
=(-2-(-1);2-2;-1-0)=(-1;0;-1)и  =(3;-3;4).
Из системы
=(3;-3;4).
Из системы
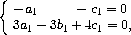
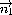 =(3;-1;-3).
Угол между плоскостями ABC и ACD равен либо углу между
их векторами нормалей, либо дополняет его до180o .
Следовательно,
=(3;-1;-3).
Угол между плоскостями ABC и ACD равен либо углу между
их векторами нормалей, либо дополняет его до180o .
Следовательно,
cos β =
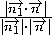 =
=
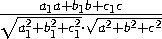 =
=
=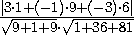 =
=  =
=
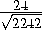 .
.
е) Через прямую AC проведём плоскость, параллельную прямой BD . Уравнение этой плоскости найдём по точке A(-1;2;0)и
вектору 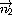 =(a2;b2;c2),
перпендикулярному векторам
=(a2;b2;c2),
перпендикулярному векторам  =(3;-3;4)и
=(3;-3;4)и 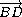 =(-7;0;0). Координаты этого вектора
найдём из системы
=(-7;0;0). Координаты этого вектора
найдём из системы
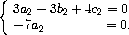
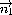 =(0;4;3).
Уравнение искомой плоскости имеет вид0(x+1)+4(y-2)+3(z-0)=0, или4y+3z-8=0.
Расстояние между прямыми BD и AC равно расстоянию от любой
точки прямой BD (например, от точки D(-2;2;-1)), параллельной AC , до проведённой плоскости, т.е.
=(0;4;3).
Уравнение искомой плоскости имеет вид0(x+1)+4(y-2)+3(z-0)=0, или4y+3z-8=0.
Расстояние между прямыми BD и AC равно расстоянию от любой
точки прямой BD (например, от точки D(-2;2;-1)), параллельной AC , до проведённой плоскости, т.е.
d=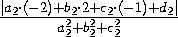 =
=
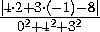 =
=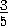 .
.
Ответ
м) 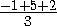 ;
╨) x+9y+6z-17=0;
у)
;
╨) x+9y+6z-17=0;
у) 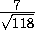 ;
Я) arccos
;
Я) arccos 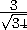 ;
ж) arccos
;
ж) arccos 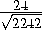 ;
и)
;
и) 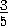 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь