Олимпиадная задача по планиметрии: нахождение стороны треугольника через описание четырёхугольника
Задача
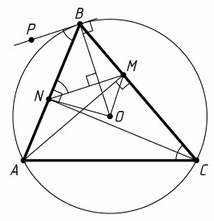
В остроугольном треугольнике ABC (AB < BC) проведены высоты AM и CN. Точка O – центр описанной окружности треугольника ABC. Известно, что ∠ABC = β, а площадь четырёхугольника NOMB равна S. Найдите сторону AC.
Решение
На касательной к описанной окружности данного треугольника отметим точку P так, чтобы она и точка C лежали по разные стороны от прямой AB. Из теоремы об угле между касательной и хордой следует, что ∠ABP = ∠C = ∠BNM, поэтому BP || MN, а так как OB ⊥ BP, то OB ⊥ MN. Треугольник BMN подобен треугольнику BAC с коэффициентом cos β, значит, MN = AC cos β.
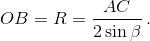 Следовательно, S= ½MN·OB= ¼AC² ctg β. Отсюда AC² = 4Stg β.
Следовательно, S= ½MN·OB= ¼AC² ctg β. Отсюда AC² = 4Stg β.
Ответ
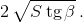
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет