Олимпиадная задача по планиметрии: площадь четырёхугольника в параллелограмме
Задача
Точка M расположена на стороне BC параллелограмма ABCD, причём BM : MC = 3 : 2. Отрезки AM и BD пересекаются в точке K. Известно, что площадь параллелограмма равна 1. Найдите площадь четырёхугольника CMKD.
Решение
Из подобия треугольников BKM и DKA находим, что BK : KD = BM : AD = BM : MC = 3 : 5. Поэтому BK : BD = 3 : 8, а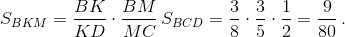 
Следовательно, SCMKD = SBCD – SBKM = ½ – 9/80 = 31/80.
Ответ
31/80.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет