Олимпиадная задача по планиметрии для 7-9 классов: отношение отрезков в треугольнике
Задача
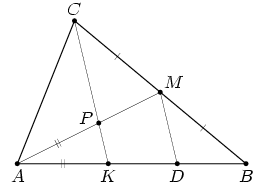
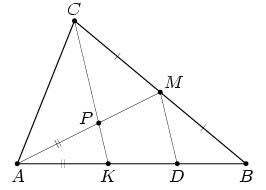
На стороне AB треугольника ABC отмечена точка K. Отрезок CK пересекает медиану AM треугольника в точке P. Оказалось, что AK = AP.
Найдите отношение BK : PM.
Решение
Первый способ. Проведём через точку M прямую, параллельную CK, которая пересечет AB в точке D (рис. слева). По теореме Фалеса BD = KD. По теореме о пропорциональных отрезках PM = KD = ½ BK.
Ответ
BK : PM = 2.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет